Z. A. H. Goodwin, V. Vitale, F. Corsetti, D. K. Efetov, A. A. Mostofi and J. Lischner, Critical role of device geometry for the phase diagram of twisted bilayer graphene, Phys. Rev. B 101, 165110 (2020).
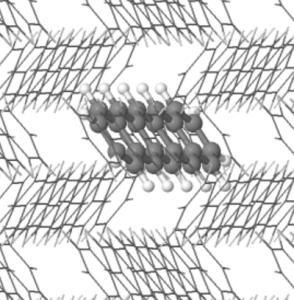
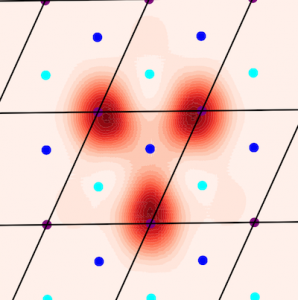
Twisted bilayer graphene (tBLG) is made of two stacked sheets of graphene that are rotated with respect to one another. The relative twist of the two layers produces a moiré pattern that forms a superlattice whose repeat length is much greater than the carbon-carbon bond length of the individual layers. For small twist angles around a “magic angle” of 1.1°, the behaviour of electrons in the moiré superlattice is fundamentally different to that of electrons in graphene or in untwisted bilayers, and tBLG is seen to exhibit unexpected insulating and superconducting states, in addition to the expected metallic state.
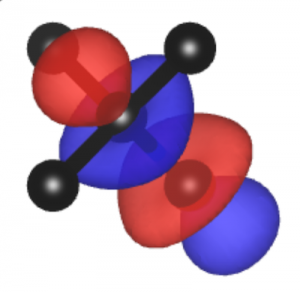
Crucially, in experiments, the tBLG is not free-standing, but is encapsulated by a thin dielectric medium which, in turn, has metallic contacts. This is extremely important, since it determines the way in which electrons in tBLG interact with one another. In a paper appearing in Physical Review B, we develop and use an electronic model of tBLG within such a device configuration. Our model captures the influence of the device geometry on the competition between phases. In particular, we show that the correlated insulator phase can be switched on or off by controlling the thickness of the dielectric layers separating tBLG from the metallic gates.
The competition between the different phases observed in tBLG makes it a rich problem, and understanding what influences it has the potential to advance our understanding of the physics of strongly-correlated electrons and unconventional superconductors.
This work was part of Zachary Goodwin’s PhD in the Centre for Doctoral Training in Theory and Simulation of Materials. Zachary is supervised by Johannes Lischner and Arash Mostofi.